攪拌器廣泛用于化工、制藥、食品、水處理、油漆、 聚合物、藥品的生產和工業廢水的凈化等工業過程。 由于缺少對混合過程的理解,經常會導致混合操作效 率低下和能耗浪費。攪拌器的功率準數是攪拌裝置 設計的**基本參數 ,決定著設備的投資和運行成 槳式、錨框式和螺帶式攪拌器功率準數的 Kamei和 Hiraoka關聯式 。 計算流體力學 (CFD)方法越來越多地用來研究 攪拌槽內的流場、混合特性以及攪拌器的功率消耗 情況
[ 4-6] 。 CFD方法可以快速方便地得到各種規模 的模擬數據, 在工業設計中的應用越來越廣泛。 本。 近年來,對攪拌器功率準數的研究不是很多。的應用也非常普遍, 也有很多關于其功率準數的文獻。 Nagata
[1] 對槳式攪拌器在無擋板、部分擋板和全擋板的條件下進行了系統的研究, 得到了槳式攪拌器功率準數的 Nagata關聯式。 Kamei等和 Hirao-ka等
[ 2-3] 基于對槳式攪拌器的實驗研究和攪拌槽內層流區槳式攪拌槳的流動數值解析的結果 , 提出了

在無擋板條件下的功率準數, 發現模擬的功率準數要小于 Nagata關聯式的功率準數。
本文通過實驗、經驗關聯式及 CFD的方法來研究單層二葉平槳、二葉斜槳、四葉斜槳以及雙層四葉斜槳的功率準數 , 并進行了對比 , 探索計算攪拌器功率準數更為準確的方法 , 為工業設計提供
依據。
1 研究方法
1.1 實驗方法
[ 7] 攪拌槽槽體為圓柱形 , 均布 4塊擋板。攪拌槽
直徑 D=0.58 m, 液位高 H=D, 雙層攪拌器時 H=
1.2D,擋板寬度為 1 /10D,離槽壁 0.008 m。攪拌槳直徑 d=0.5 -0.6D, 槳葉離底距離 C=0.35D, 雙層攪拌器時 C=0.3D, 2 層攪拌槳軸向中心距離為0.6D。槳式攪拌器詳細參數見表 1, 表中 b為攪拌槳的寬度, m;np為一層槳葉的葉片數量 ,個 ;θ為斜槳槳葉與水平面的傾斜角 , (°)。
表 1 槳葉名稱及結構參數比
Table1 Nameandstructureparametersratioofimpellers
|
|
|
d/D |
b/d |
C/D |
p |
θ/(°) |
|
|
編號 |
名稱 |
|
|
|
n |
|
|
|
1 |
二葉平槳 |
0.6 |
0.109 0.35 |
2 |
90 |
|
|
2 |
二葉斜槳 |
0.6 |
0.109 |
0.35 |
2 |
45 |
|
|
3 |
四葉斜槳 |
0.6 |
0.092 |
0.35 |
4 |
45 |
|
|
4 |
2層四葉斜槳 |
0.5 |
0.083 |
0.30 |
4 |
45 |
|
攪拌槽內雷諾數按 Re=rd
2ρ/μ計算 , ρ為物料的密度 , μ為物料黏度, r為攪拌器旋轉的速度。功率消耗 P通過測量攪拌器的扭矩 M獲得, 功率 P=
2πrM,功率準數 NP =P/ρr
3d
5。
1.2 關聯方法通過關聯式來計算攪拌器功率準數也是一種常
用的方法,它具有簡單、快速的優點。對于槳式攪拌器功率準數的關聯式主要有 Nagata關聯式和 Kamei
和 Hiraoka關聯式。
1.2.1 Nagata關聯式
無擋板條件 :
NP0 =A/Re+B[ (1 000 +1.2Re
0.66 )/ (1 000 +3.2Re
0.66 )]
p(H/D)
(0.35 +b/D)sin
1.2 θ
式中:A=14 +(b/D)[ 670(d/D-0.6)
2 +185]
B=10[ 1.3 -4(b/D-0.5)2 -1.14(d/D)]
p=1.1 +4(b/D)-2.5(d/D-2.5)
2 -7(b/D)
4 Re=Nd
2ρ/μ
全擋板條件 :
NPmax的計算通過無擋板 NP0計算式中的 Re用Reθ代替,即可求出。
Reθ=10
4(1 -sinθ)25(d/D-0.4)
2 /(b/D)+ (b/D)/[ 0.11(b/D)-0.004 8]

部分擋板條件 :
(NPmax-NP)/(NPmax-NP0 )=[ 1 -2.9(Bw/D)
1.2 nb]
2 1.2.2 Kamei和 Hiraoka關聯式
無擋板條件:


|
|
4 |
2 |
|
3 |
2 |
f |
|
|
|
NP0 = [ 1.2π β ] /[ |
8d/(DH)] |
|
|
式中 |
: f=CL/Re+C [ (C /Re)+Re] |
-1 |
+ |
|
|
|
G t |
|
tr |
G |
G |
|
|
|
|
|
|
|
|
|
∞ |
t 1/m |
m |
|
|
|
|
|
(f/C) |
|
|
|
|
|




ReG = [ πηln(D/d)] /(4d/βD) Re
CL=0.215ηn(d/H)[p 1 -(d/D)
2] + 1.83(bsinθ/H)(np/2sinθ)
1/3
Ct=[ (1.96X
1.19 )
-7.8 +(0.25)
-7.8 ]
-1 /7.8
|
m=[ (0.71X0.373 )-7.8 |
+(0.333)-7.8 ] -1/7.8 |
|
|
Ctr=23.8(d/D)-3.24 (bsinθ/D)-1.18 X-0.74 |
|
|
∞ |
0 015 1 |
|
|
|
|
|
|
0.308 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
f = . |
(d/D)C |
|
|
|
|
|
|
|
|
|
0.71.6 |
θ/H |
|
|
|
|
|
|
|
|
|
|
X=γn bsin |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β =2ln(D/d)/[ (D/d)-(d/D)] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
1/3 |
|
|
|
|
|
γ=[ ηln(D/d)/(βD/d)] |
|
|
|
|
|
|
|
|
0 711 |
0 157 |
|
|
|
p |
|
|
|
|
0.611 |
/ |
|
|
η= . . |
|
|
+[ nln(D/d)] |
|
|
|
|
|
|
0.52 |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
p |
|
-(d/D)] |
|
|
|
|
|
|
|
n [ |
|
|
|
|
|
|
|
全擋板條件: |
|
0.7 |
|
1.3 |
|
0.7 |
|
|
|
|
|
平槳 |
|
10 |
|
|
|
|
0 |
54 |
|
|
p |
|
|
|
|
p |
|
|
|
|
:NPmax= (n b/d) , (n b/d)≤ . |
|
|
8 3 |
|
0.7 |
|
|
|
|
0 54 |
|
0.7 |
|
|
1 |
6 |
|
|
|
p |
|
|
|
|
|
p |
|
|
|
NPmax= .(n b/d), . |
|
|
<(n b/d)≤ . |
|
|
10 |
0.7 |
|
|
|
|
0 |
6 1 |
6 |
0.7 |
|
|
|
|
|
p |
|
|
|
|
p |
|
|
|
|
|
NPmax= (n b/d)., . <(n b/d) |
|
|
斜槳 |
|
8 3 |
2 |
|
0.9 |
|
|
0.7 |
|
1.6 |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
:NPmax= .(θ/π) (n bsin θ/d) |
|
部分擋板條件 : |
|
|
|
-3 -1 /3 |
|
|
|
|
|
|
|
NP =[ (1 |
|
|
|
] NPmax |
|
|
|
|
|
+x ) |
|
|
|
|
|
|
|
4 5 |
|
|
|
|
|
0.8 |
0.2 |
|
|
0 |
/NPmax |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
x= .(Bw/D)n /NPmax |
+NP |
|
|



雙層槳式攪拌器功率準數計算方法見文獻[ 8] 。 1.3 模擬方法 1.3.1 攪拌槽結構網格劃分
取整個槽體進行建模, 采用四面體單元進行離散, 對槽體靜止體系部分, 槳葉旋轉部分分別劃網格, 單層共劃分了 55萬個左右的網格, 雙層共 67萬個左右的網格。為增加計算的精確度, 對槳葉、交界面、近壁區采取網格加密處理。
1.3.2 計算方法計算使用的軟件是 FLUENT6.3。壓力-速度耦
合使用 SIMPLE算法得到 ,差分格式采用二階迎風,流動場的計算采用多重參考系法 (MRF)。計算中對層流區、過渡流區和湍流區采用不同的方法進行模擬。湍流區域采用標準 k-ε模型計算。由于目前還沒有專門針對過渡流區的計算模型, 本文分別采用了標準 k-ε模型。
2 結果與討論
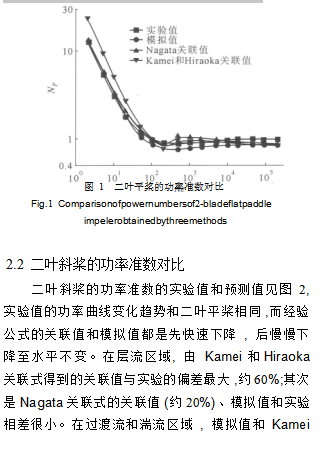
2.1 二葉平槳的功率準數對比從圖 1可以看出,實驗值和模擬值的功率曲線具
有相同的趨勢,功率準數都是隨著雷諾數的增加先降低后緩慢增加。而利用經驗公式關聯得到的功率曲線的變化趨勢都是先下降后增加,再緩慢下降。在層流區域,模擬值以及 Nagata關聯式的關聯值和實驗值吻合很好,而 Kamei和 Hiraoka關聯式的關聯值比實驗值大 0.5— 0.7倍。在過渡流區域 ,模擬值和 Na-gata關聯式的關聯值與實驗偏差約 15%,而 Kamei和Hiraoka關聯式的關聯值與實驗值吻合較好。在湍流區域 ,模擬值與不同關聯值相差很小,都比實驗值小
10%— 15%。利用 Nagata關聯式和 CFD方法能夠在
比較寬泛的雷諾數區域比較準確地預測二葉平槳的功率準數, Kamei和 Hiraoka關聯式能夠對過渡流和湍流區域的功率準數進行合理的預測。
2.3 4葉斜槳的功率準數對比利用 Nagata關聯式計算低雷諾數四葉斜槳的
功率準數時采用等面積的辦法。
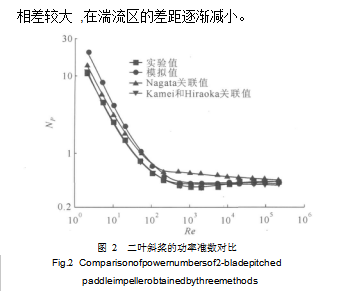
從圖 3發現 , 在層流區域, 模擬值和 Nagata關聯式的關聯值與實驗值吻合很好, Kamei和 Hiraoka 關聯式的關聯值與實驗值相差 30%—50%。在過渡流和湍流區域時 , 模擬值和 Kamei和 Hiraoka關聯式的關聯值與實驗值相差較小, 而 Nagata關聯式的關聯值與實驗值相差 30%— 60%。這說明 Nagata 關聯式在有擋板和雷諾數較小的情況下 ,采用等面積法進行攪拌器的功率準數有效 , 而在雷諾數較大時, 由于流體流動情況的改變 ,采用等面積的方法預測攪拌器的功率準數要偏大很多。

圖 3 四葉斜槳的功率準數對比
Fig.3 Comparisonofpowernumbersof4-bladepitched
paddleimpellerobtainedbythreemethods
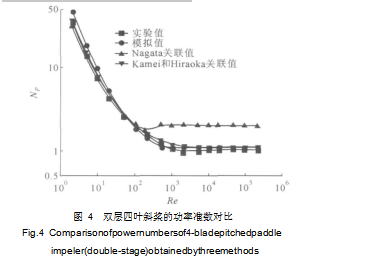
2.4 雙層四葉斜槳的功率準數對比從圖 4可以看出,在層流區域 ,模擬值和 Nagata
關聯式的關聯值吻合較好, Kame和 Hiraoka關聯式的關聯值與實驗值的偏差 20%—30%。在過渡流
區域, 模擬值和 Kamei和 Hiraoka關聯式相差 15%
左右, 在湍流區域 ,模擬值和 Kamei和 Hiraoka關聯式與實驗值相差較小。 Nagata關聯式的關聯值與實驗值在過渡流和湍流區域二者相差約 90%, 雙層四葉斜槳在層流區域雙層按單層的 2 倍是有效的 ,在過渡流和湍流時由于流型的改變, 雙層槳的關聯功率值則偏大。
3 結論
(1)Nagata關聯式在層流狀態時關聯值與實驗值相差較小 , 在湍流時二者相差較大 ;Kamei和Hiraoka關聯式則在過渡流和湍流區與實驗值比較吻合, 在層流區的偏差比較大。因此 ,在層流區域宜采用 Nagata關聯式,而在過渡流和湍流區域宜采用Kamei和 Hiraoka關聯式對槳式攪拌器的功率準數進行關聯。
(2)利用 CFD模擬了攪拌器各種狀態的功率準數值, 模擬值與實驗值對比發現 ,模擬值在不同的雷諾數時都與實驗值吻合較好 ,計算流體力學方法能夠較為準確地預測攪拌器的功率準數。
符號說明:
b 槳葉寬度 , m
B
w 檔板寬度, m D 攪拌槽直徑, m



